Well December 22nd has come and gone, and the promised release of Planck data has, perhaps unsurprisingly, not materialised. Some of the talks presented at the Ferrara conference are available here, and there was a second conference in Paris more recently, video recordings from which can be found here.
I've seen a bit of speculation about the delays and what the data might or might not be showing on a few physics blogs, some of which I think are a little mistaken. So I thought I'd put up a quick post summarising the situation as I see it — but note that my opinion is not at all official and may be wrong on some of the details (especially since I wasn't at either of the conferences).
For a start, you may notice that some of the talks at Ferrara are not made available on the website. I'm informed that this internal censorship was applied by the Planck science team, and it is based on their estimation that the censored talks are ones containing results which are still preliminary and liable to change before the eventual data release. The flip side of this is that the talks that are available contain data which they are confident will not change, so these are the ones you'd want to pay attention to in any case.
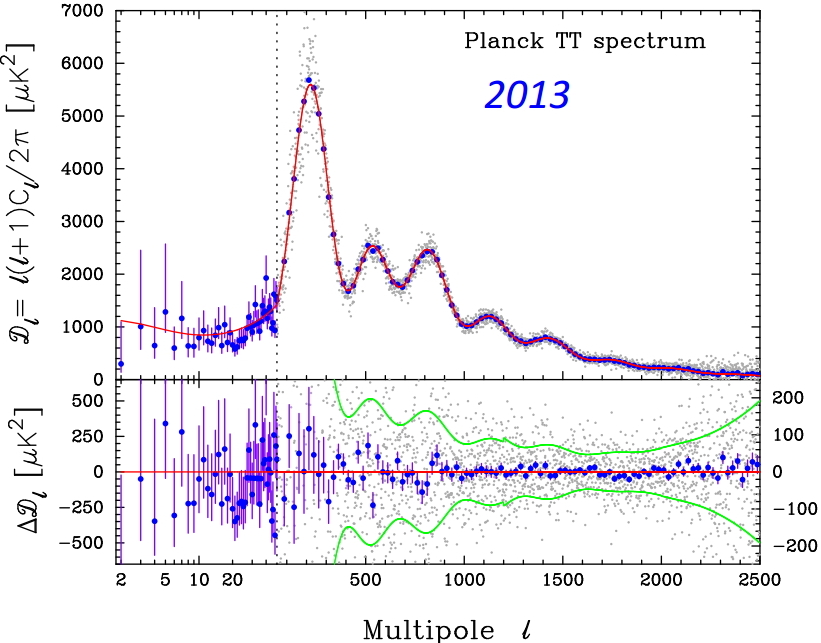
In terms of the data itself, there appear to be two and a half important improvements so far. The first is that the overall calibration of the temperature power spectrum — which was previously somewhat discrepant with the WMAP measurement — has been improved, and now Planck and WMAP agree very well with each other. The second is that the apparent anomaly in the temperature power spectrum at multipole values of $\ell\sim1800$ has been identified as being due to a glitch in the 217 GHz data, and has been corrected. The anomaly has therefore disappeared. This can be seen by comparing the 2013 and 2014 versions of the TT power (if you look carefully):
The remaining half an improvement comes from the polarization data. Previously, this was so badly affected by systematics at large scales that the Planck team were only able to even show the data points at $\ell>100$, and were unable to use them for any science analysis, relying instead on the WMAP polarization. These systematics have still not been completely resolved — apparently it is the HFI instrument which is the problematic one — but they have been somewhat improved, such that the EE and TE power spectra are trustworthy at $\ell>30$, which is enough to start using them for parameter constraints in place of the WMAP data. (This means that the error bars on various derived parameter values have decreased a little from 2013, but they will decrease a lot more when all the data is finally available.)
This last half improvement is somewhat relevant to the BICEP2 issue which I discussed here, since the improved polarization data in 2014 was an important reason that Planck was able to say something about the dust polarization in the BICEP2 window. The fact that they still aren't 100% happy with this data yet could be a bit concerning. On the other hand, the relevant range of multipoles for BICEP2 is $\ell\sim80$ rather than $\ell<30$.
In terms of what these new data tell us, I'm afraid the story appears mostly rather boring, since there is very little change from what we learned already in 2013. As expected, the values of all cosmological parameters are consistent with what Planck announced in 2013; insofar as there have been any minor changes in the values, they tend to move in the direction of making Planck and WMAP more consistent with each other, but really these shifts appear very small and not worth worrying about. It appears the only parameter which has shifted at all significantly is the optical depth $\tau$. Constraints on $\tau$ rely on the use of polarization data; the previous constraints were obtained by combining Planck temperature with WMAP polarization measurements whereas the current value comes from Planck alone.
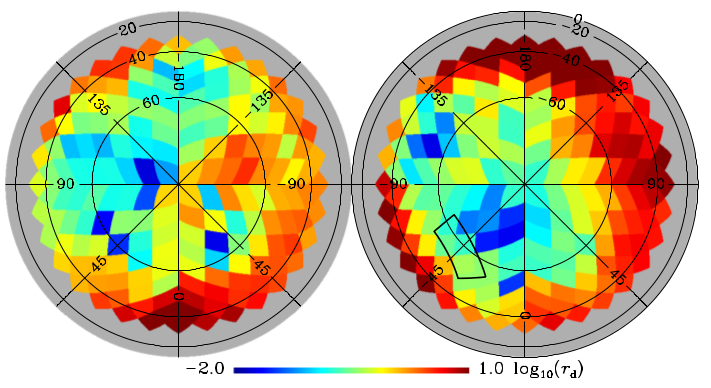
At some point I suppose the various systematics with the HFI polarization data will be sorted out to the extent that we will get the long-awaited release and the papers. But I have given up trying to predict when. In the meantime, I thought the coolest thing to come out of the recent conferences was this image:
which rather reminded me of this:
and this:
I've seen a bit of speculation about the delays and what the data might or might not be showing on a few physics blogs, some of which I think are a little mistaken. So I thought I'd put up a quick post summarising the situation as I see it — but note that my opinion is not at all official and may be wrong on some of the details (especially since I wasn't at either of the conferences).
For a start, you may notice that some of the talks at Ferrara are not made available on the website. I'm informed that this internal censorship was applied by the Planck science team, and it is based on their estimation that the censored talks are ones containing results which are still preliminary and liable to change before the eventual data release. The flip side of this is that the talks that are available contain data which they are confident will not change, so these are the ones you'd want to pay attention to in any case.
In terms of the data itself, there appear to be two and a half important improvements so far. The first is that the overall calibration of the temperature power spectrum — which was previously somewhat discrepant with the WMAP measurement — has been improved, and now Planck and WMAP agree very well with each other. The second is that the apparent anomaly in the temperature power spectrum at multipole values of $\ell\sim1800$ has been identified as being due to a glitch in the 217 GHz data, and has been corrected. The anomaly has therefore disappeared. This can be seen by comparing the 2013 and 2014 versions of the TT power (if you look carefully):
The remaining half an improvement comes from the polarization data. Previously, this was so badly affected by systematics at large scales that the Planck team were only able to even show the data points at $\ell>100$, and were unable to use them for any science analysis, relying instead on the WMAP polarization. These systematics have still not been completely resolved — apparently it is the HFI instrument which is the problematic one — but they have been somewhat improved, such that the EE and TE power spectra are trustworthy at $\ell>30$, which is enough to start using them for parameter constraints in place of the WMAP data. (This means that the error bars on various derived parameter values have decreased a little from 2013, but they will decrease a lot more when all the data is finally available.)
This last half improvement is somewhat relevant to the BICEP2 issue which I discussed here, since the improved polarization data in 2014 was an important reason that Planck was able to say something about the dust polarization in the BICEP2 window. The fact that they still aren't 100% happy with this data yet could be a bit concerning. On the other hand, the relevant range of multipoles for BICEP2 is $\ell\sim80$ rather than $\ell<30$.
In terms of what these new data tell us, I'm afraid the story appears mostly rather boring, since there is very little change from what we learned already in 2013. As expected, the values of all cosmological parameters are consistent with what Planck announced in 2013; insofar as there have been any minor changes in the values, they tend to move in the direction of making Planck and WMAP more consistent with each other, but really these shifts appear very small and not worth worrying about. It appears the only parameter which has shifted at all significantly is the optical depth $\tau$. Constraints on $\tau$ rely on the use of polarization data; the previous constraints were obtained by combining Planck temperature with WMAP polarization measurements whereas the current value comes from Planck alone.
At some point I suppose the various systematics with the HFI polarization data will be sorted out to the extent that we will get the long-awaited release and the papers. But I have given up trying to predict when. In the meantime, I thought the coolest thing to come out of the recent conferences was this image:
which rather reminded me of this:
 |
| Detail from The Starry Night. |
 |
| Detail from Haystacks Near a Farm in Provence. |