About two weeks ago, I mentioned a recently published paper by Chilean authors Moni Bidin et al., claiming to have found no evidence for dark matter around our local neighbourhood in the Milky Way. Very soon afterwards, I pointed out a new pre-print by Bovy and Tremaine that rebutted this claim. Although I suppose I was fairly quickly on the scene, I wasn't particularly happy with the way I had reported this argument: just mentioning that some people disagree with each other without any explanation of the reasons is a bit closer to mere journalism than I was intending.
Since then, there have been several blog posts on this issue elsewhere — see Résonaances, Peter Coles, Matt Strassler and Sean Carroll among others — but to be honest I didn't think they actually did much more than report that people disagreed with each other either (although many of them did add some sociological comments). Which is fine as far as it goes, but if you were looking for someone to explain the science to you, you might have been disappointed. Jon Butterworth at least made a commendable effort in his Guardian blog, but he was perhaps limited by space and an inability to include any mathematics. In the end he simply said that he believed the Bovy and Tremaine result because Peter Coles believed it (and Peter Coles essentially told us to believe it because Scott Tremaine is an acknowledged world expert in galactic dynamics). Which is all very good and probably correct, but not very enlightening!1
So eventually I've decided to fill this gap in the market myself: this post will attempt to summarise and explain both papers to a non-expert (i.e. anyone who doesn't actually work in the field of galactic dynamics). A major caveat before I start: I don't work in galactic dynamics either. I don't own, and had never read, the main reference work on this subject (by Binney and Tremaine; you see why people might trust Tremaine to be right on this one!). In preparation for writing this post I borrowed a copy and read a small amount of it — enough to feel I understood what was going on — but even so much of what I am about to write might be over-simplified, misrepresented or simply wrong. If you happen to spot any mistakes, please let me know.
Now that we've got that out of the way, let's start.
Most people who have read this far probably already know that our galaxy, the Milky Way, is a spiral galaxy, which means that the normal baryonic matter (which is mostly hydrogen and helium, in the form of both stars and interstellar gas) is arranged in a relatively thin flat disk with spiral arms. There's a central bulge with older stars, and a supermassive black hole right at the very centre, but that's not important for the moment. Here's a front-on picture of spiral galaxy NGC 5457; the Milky Way would look somewhat similar if we could get outside it to see it.
However, we believe — for a whole variety of reasons — that this luminous matter is only a small fraction of the total mass of any galaxy. The remaining dark matter is non-baryonic, doesn't shine, and interacts only very weakly with the baryonic matter, so it has only been detected so far through its gravitational influence on the dynamics of the matter that we do see. The dark matter is not arranged in a disk like the baryonic matter; instead it forms a roughly spherical halo around the visible part of the galaxy and extending much farther out than it. This is a cartoon to illustrate a side-on view of the Milky Way:
In what follows I will use a cylindrical coordinate system $(R,\phi,z)$, with the galactic centre at the origin. The Sun lies in the disk, about $R_0=8$ kiloparsecs from the centre of the galaxy [a kiloparsec is $3260$ light years, or $3.1\times10^{16}$ kilometres]. The total thickness of the disk at the solar location is about $2-3$ kpc. We don't actually know very much about the shape of the dark matter halo or about how the density of dark matter changes with distance from the centre. There are several different models of the halo mass distribution but observations can't yet distinguish between them.
Moni Bidin et al.'s method of determining the dark matter density at our location was to try measure the integrated surface density, defined by $$\Sigma(Z)\equiv\int_{-Z}^{Z}dz\;\rho(z)\,,$$ where $\rho(z)$ is the total matter density at radius $R_0$ in the solar vicinity. Assuming symmetry on either side of the galactic plane means we need only bother with positive $Z$.
$\Sigma(Z)$ contains contributions from both baryonic and dark matter, but since almost all of the baryonic mass lies within the disk, at heights $Z>2$ kpc the baryonic contribution to the integrand drops to essentially zero. If no dark matter were present, $\Sigma(Z)$ should therefore be a constant above this height. In the usual models of the dark matter halo, on the other hand, $\Sigma(Z)$ continues to increase linearly with height, with the slope dependent on the details of the model.
So the way to check for a contribution from dark matter is to measure $\Sigma(Z)$ at various heights and check to see if it keeps increasing at $Z>2$ kpc. It's particularly important to get out to large values of $Z$ because otherwise the baryonic contribution is still non-zero and as we don't know exactly what non-zero value it should have the uncertainty introduced is too much to make any useful statements.2
The question is then how to measure $\Sigma(Z)$ at large enough heights. Well, the Poisson equation relates the mass density to derivatives of the gravitational potential, and as $\Sigma(Z)$ is an integral over the mass density and the derivatives of the gravitational potential can be written in terms of the components of the force acting on objects at any location, we can obtain an equation for $\Sigma(Z)$ in terms of these force components. I won't write it down here.
The components of the force at a location in the galaxy, denoted $F_R$ and $F_Z$, determine the dynamics of stars there. What Moni Bidin and collaborators did was to identify a group of 412 stars that lay at large enough heights above the galactic plane that by observing their velocities they could calculate $F_R$ and $F_Z$, and then in turn calculate $\Sigma(Z)$. Treating the galaxy as a virialised system in a steady state allows one to use the Jeans equation to describe the force components in terms of observed velocities of the tracer population of stars. The point of contention is how they determined $F_R$ from the observed velocities.
Instead of using $F_R$, it is more convenient to describe things in terms of the circular speed $V_c(R)$, defined by $V_c^2=-RF_R$. The circular speed is essentially the rotational speed with which a star at distance $R$ from the centre of the galaxy would move if it were on a circular orbit about the galactic centre. Actually stars aren't on circular orbits but elliptical ones, so they have a rotational velocity $V_\phi$ which is different from $V_c$. Individual stars all have different orbits, so actually we need to deal with average quantities for the tracer population of 412 stars, in particular the mean azimuthal (or rotational) velocity $\bar{V}_\phi(R,Z)$.
There is a difference between $\bar{V}_\phi$ and $V_c$ as well, called the 'asymmetric drift'. This is because of two factors. Firstly, stars on the outer part of an elliptical orbit have a smaller rotational velocity than when they are on the section of the ellipse closer to the galactic centre. Since the density of stars decreases as you go away from the centre, more of the stars at the solar radius are 'inner' stars on the outer part of their orbit than 'outer' stars on the inner part of their orbit. Secondly, the dispersion in the velocities of a population of 'inner' stars is greater than that of 'outer' stars.3 The radial Jeans equation then specifies the difference between $\bar{V}_\phi$ and $V_c$ in terms of quantities related to the density of the tracer stars and their velocity dispersion.
To make further progress in calculating $F_R$ as a function of $Z$ (and thus $\Sigma(Z)$) from the observed value of $\bar{V}_\phi$, several assumptions need to be made about how the velocity dispersion and the tracer density change with radius and height above the disk. In fact, Moni Bidin et al. list a total of 11 assumptions they make, of which 10 are apparently more or less reasonable and seem to roughly agree with observations. The key assumption that Bovy and Tremaine claim is not reasonable is that the "rotation curve is locally flat", i.e. $$\frac{\partial \bar{V}_\phi}{\partial R}=0$$ at all relevant values of $Z$.
As I understand it, when people say the rotation curve is flat, they normally mean the circular speed doesn't change with radius, i.e. $\partial V_c/\partial R=0$. This has been measured and we know it is roughly true away from the very centre of the galaxy (in fact the flatness of the circular speed curve is one reason why we need dark matter in models of galaxies). But this assumption is crucially different! Moni Bidin et al. later on in their paper relax this assumption and calculate how non-flat the azimuthal velocity curve would need to be in order for their data to be compatible with the usual models of the dark matter halo. They dismiss the value they obtain as impossible, and cite some papers they claim have demonstrated that the curve is indeed essentially flat.
I skimmed through these references and as far as I can tell, they only ever refer to the circular speed curve, never to the azimuthal velocity curve. As far as I know, there are no measurements of how the azimuthal velocity curve behaves, only the circular speed curve. So this seems to be a simple error of reading comprehension! In fact Bovy and Tremaine show that if the azimuthal velocity curve were indeed flat, the circular speed curve would have a strange behaviour, in contradiction with observations.
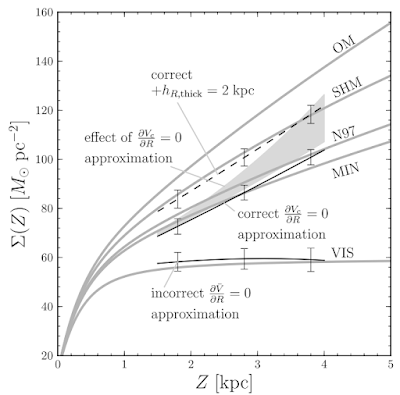
Here is a figure to demonstrate the effect of this assumption. It shows $\Sigma(R_0,Z)$ as a function of $Z$. The thick grey curves are theoretical, based on various models for the dark matter halo; the one labelled VIS assumes that there is no dark matter halo at all. The lower, flat, black line and data points is what you get when you interpret the Moni Bidin observations assuming $\partial \bar{V}_\phi/\partial R=0$ — consistent with no dark matter. Instead if you assume $\partial V_c/\partial R=0$ you get the upper solid black curve. Changing a few other assumptions produces the dashed black curve or the shaded grey region. So basically consistent with many of the halo models!
All in all this is really a bit of a shame for the Chileans. Firstly of course because they had a big press conference to announce their result, and now it turns out to be wrong. (Yes, I'm pretty convinced it is wrong.) Secondly because the reason it was wrong was because of a mistake that could really have been spotted and corrected before the press release (and should have been spotted by the ApJ referee who appears to have focussed on various other less relevant things instead!). But mostly it is sad because their method is quite a good one: in fact interpreted correctly it gives the best measurement of the dark matter density yet. They've obviously done good work identifying those 412 stars and measuring their velocities, they just somehow got the wrong answer out at the end. In fact they even got the right answer in their paper but dismissed it as implausible!
I also sort of want to defend them against many of the comments I have seen online. Neither their paper nor their press conference really contain any evidence that they are the loony "dark matter deniers" some people have painted them as. They very clearly stated their assumptions, and their reasons for believing them, and then the logical conclusions that followed. That the assumptions turned out to be wrong is unfortunate, but far better to be methodical and clear in that manner than a lot of other rubbish you see on the arXiv. This allows science to progress faster!
If I were to draw one moral from this long story it would be that you shouldn't place too much faith in peer review by journal referees. Referees often don't read papers carefully enough, with the result that publication ends up depending on their gut feeling about the result rather than the details of the science presented therein. Gut feelings are often wrong. Hence why more transparency in the review process might be a better idea!
1 I don't want to sound critical of these other bloggers: none of them work on galactic dynamics professionally so it's perfectly natural that they shouldn't write detailed posts about it. I decided to write this mostly because it gave me a reason to learn a little bit about a new field, and to procrastinate from other stuff I was meant to do.
2 This method can only tell you about the dark matter density exactly at our location if you make some further assumptions about how this density varies with height and extrapolate to $Z\simeq0$. That's fine; if we could definitely say the existing halo models were wrong that would be exciting enough even without being certain exactly what was happening at our location.
3 Binney and Tremaine provide a nice analogy: "there are more Japanese than Nepalese in Oxford in the summer, both because the population of Japan exceeds that of Nepal, and because Japanese have larger travel budgets than Nepalese."
Since then, there have been several blog posts on this issue elsewhere — see Résonaances, Peter Coles, Matt Strassler and Sean Carroll among others — but to be honest I didn't think they actually did much more than report that people disagreed with each other either (although many of them did add some sociological comments). Which is fine as far as it goes, but if you were looking for someone to explain the science to you, you might have been disappointed. Jon Butterworth at least made a commendable effort in his Guardian blog, but he was perhaps limited by space and an inability to include any mathematics. In the end he simply said that he believed the Bovy and Tremaine result because Peter Coles believed it (and Peter Coles essentially told us to believe it because Scott Tremaine is an acknowledged world expert in galactic dynamics). Which is all very good and probably correct, but not very enlightening!1
So eventually I've decided to fill this gap in the market myself: this post will attempt to summarise and explain both papers to a non-expert (i.e. anyone who doesn't actually work in the field of galactic dynamics). A major caveat before I start: I don't work in galactic dynamics either. I don't own, and had never read, the main reference work on this subject (by Binney and Tremaine; you see why people might trust Tremaine to be right on this one!). In preparation for writing this post I borrowed a copy and read a small amount of it — enough to feel I understood what was going on — but even so much of what I am about to write might be over-simplified, misrepresented or simply wrong. If you happen to spot any mistakes, please let me know.
Now that we've got that out of the way, let's start.
Most people who have read this far probably already know that our galaxy, the Milky Way, is a spiral galaxy, which means that the normal baryonic matter (which is mostly hydrogen and helium, in the form of both stars and interstellar gas) is arranged in a relatively thin flat disk with spiral arms. There's a central bulge with older stars, and a supermassive black hole right at the very centre, but that's not important for the moment. Here's a front-on picture of spiral galaxy NGC 5457; the Milky Way would look somewhat similar if we could get outside it to see it.
 |
| Figure 1: Spiral galaxy NGC 5457 viewed front-on. |
However, we believe — for a whole variety of reasons — that this luminous matter is only a small fraction of the total mass of any galaxy. The remaining dark matter is non-baryonic, doesn't shine, and interacts only very weakly with the baryonic matter, so it has only been detected so far through its gravitational influence on the dynamics of the matter that we do see. The dark matter is not arranged in a disk like the baryonic matter; instead it forms a roughly spherical halo around the visible part of the galaxy and extending much farther out than it. This is a cartoon to illustrate a side-on view of the Milky Way:
In what follows I will use a cylindrical coordinate system $(R,\phi,z)$, with the galactic centre at the origin. The Sun lies in the disk, about $R_0=8$ kiloparsecs from the centre of the galaxy [a kiloparsec is $3260$ light years, or $3.1\times10^{16}$ kilometres]. The total thickness of the disk at the solar location is about $2-3$ kpc. We don't actually know very much about the shape of the dark matter halo or about how the density of dark matter changes with distance from the centre. There are several different models of the halo mass distribution but observations can't yet distinguish between them.
Moni Bidin et al.'s method of determining the dark matter density at our location was to try measure the integrated surface density, defined by $$\Sigma(Z)\equiv\int_{-Z}^{Z}dz\;\rho(z)\,,$$ where $\rho(z)$ is the total matter density at radius $R_0$ in the solar vicinity. Assuming symmetry on either side of the galactic plane means we need only bother with positive $Z$.
$\Sigma(Z)$ contains contributions from both baryonic and dark matter, but since almost all of the baryonic mass lies within the disk, at heights $Z>2$ kpc the baryonic contribution to the integrand drops to essentially zero. If no dark matter were present, $\Sigma(Z)$ should therefore be a constant above this height. In the usual models of the dark matter halo, on the other hand, $\Sigma(Z)$ continues to increase linearly with height, with the slope dependent on the details of the model.
So the way to check for a contribution from dark matter is to measure $\Sigma(Z)$ at various heights and check to see if it keeps increasing at $Z>2$ kpc. It's particularly important to get out to large values of $Z$ because otherwise the baryonic contribution is still non-zero and as we don't know exactly what non-zero value it should have the uncertainty introduced is too much to make any useful statements.2
The question is then how to measure $\Sigma(Z)$ at large enough heights. Well, the Poisson equation relates the mass density to derivatives of the gravitational potential, and as $\Sigma(Z)$ is an integral over the mass density and the derivatives of the gravitational potential can be written in terms of the components of the force acting on objects at any location, we can obtain an equation for $\Sigma(Z)$ in terms of these force components. I won't write it down here.
The components of the force at a location in the galaxy, denoted $F_R$ and $F_Z$, determine the dynamics of stars there. What Moni Bidin and collaborators did was to identify a group of 412 stars that lay at large enough heights above the galactic plane that by observing their velocities they could calculate $F_R$ and $F_Z$, and then in turn calculate $\Sigma(Z)$. Treating the galaxy as a virialised system in a steady state allows one to use the Jeans equation to describe the force components in terms of observed velocities of the tracer population of stars. The point of contention is how they determined $F_R$ from the observed velocities.
Instead of using $F_R$, it is more convenient to describe things in terms of the circular speed $V_c(R)$, defined by $V_c^2=-RF_R$. The circular speed is essentially the rotational speed with which a star at distance $R$ from the centre of the galaxy would move if it were on a circular orbit about the galactic centre. Actually stars aren't on circular orbits but elliptical ones, so they have a rotational velocity $V_\phi$ which is different from $V_c$. Individual stars all have different orbits, so actually we need to deal with average quantities for the tracer population of 412 stars, in particular the mean azimuthal (or rotational) velocity $\bar{V}_\phi(R,Z)$.
There is a difference between $\bar{V}_\phi$ and $V_c$ as well, called the 'asymmetric drift'. This is because of two factors. Firstly, stars on the outer part of an elliptical orbit have a smaller rotational velocity than when they are on the section of the ellipse closer to the galactic centre. Since the density of stars decreases as you go away from the centre, more of the stars at the solar radius are 'inner' stars on the outer part of their orbit than 'outer' stars on the inner part of their orbit. Secondly, the dispersion in the velocities of a population of 'inner' stars is greater than that of 'outer' stars.3 The radial Jeans equation then specifies the difference between $\bar{V}_\phi$ and $V_c$ in terms of quantities related to the density of the tracer stars and their velocity dispersion.
To make further progress in calculating $F_R$ as a function of $Z$ (and thus $\Sigma(Z)$) from the observed value of $\bar{V}_\phi$, several assumptions need to be made about how the velocity dispersion and the tracer density change with radius and height above the disk. In fact, Moni Bidin et al. list a total of 11 assumptions they make, of which 10 are apparently more or less reasonable and seem to roughly agree with observations. The key assumption that Bovy and Tremaine claim is not reasonable is that the "rotation curve is locally flat", i.e. $$\frac{\partial \bar{V}_\phi}{\partial R}=0$$ at all relevant values of $Z$.
As I understand it, when people say the rotation curve is flat, they normally mean the circular speed doesn't change with radius, i.e. $\partial V_c/\partial R=0$. This has been measured and we know it is roughly true away from the very centre of the galaxy (in fact the flatness of the circular speed curve is one reason why we need dark matter in models of galaxies). But this assumption is crucially different! Moni Bidin et al. later on in their paper relax this assumption and calculate how non-flat the azimuthal velocity curve would need to be in order for their data to be compatible with the usual models of the dark matter halo. They dismiss the value they obtain as impossible, and cite some papers they claim have demonstrated that the curve is indeed essentially flat.
I skimmed through these references and as far as I can tell, they only ever refer to the circular speed curve, never to the azimuthal velocity curve. As far as I know, there are no measurements of how the azimuthal velocity curve behaves, only the circular speed curve. So this seems to be a simple error of reading comprehension! In fact Bovy and Tremaine show that if the azimuthal velocity curve were indeed flat, the circular speed curve would have a strange behaviour, in contradiction with observations.
Here is a figure to demonstrate the effect of this assumption. It shows $\Sigma(R_0,Z)$ as a function of $Z$. The thick grey curves are theoretical, based on various models for the dark matter halo; the one labelled VIS assumes that there is no dark matter halo at all. The lower, flat, black line and data points is what you get when you interpret the Moni Bidin observations assuming $\partial \bar{V}_\phi/\partial R=0$ — consistent with no dark matter. Instead if you assume $\partial V_c/\partial R=0$ you get the upper solid black curve. Changing a few other assumptions produces the dashed black curve or the shaded grey region. So basically consistent with many of the halo models!
 |
| Figure 3: Surface density integral as a function of height above the galactic plane. Taken from arXiv:1205.4033. |
All in all this is really a bit of a shame for the Chileans. Firstly of course because they had a big press conference to announce their result, and now it turns out to be wrong. (Yes, I'm pretty convinced it is wrong.) Secondly because the reason it was wrong was because of a mistake that could really have been spotted and corrected before the press release (and should have been spotted by the ApJ referee who appears to have focussed on various other less relevant things instead!). But mostly it is sad because their method is quite a good one: in fact interpreted correctly it gives the best measurement of the dark matter density yet. They've obviously done good work identifying those 412 stars and measuring their velocities, they just somehow got the wrong answer out at the end. In fact they even got the right answer in their paper but dismissed it as implausible!
I also sort of want to defend them against many of the comments I have seen online. Neither their paper nor their press conference really contain any evidence that they are the loony "dark matter deniers" some people have painted them as. They very clearly stated their assumptions, and their reasons for believing them, and then the logical conclusions that followed. That the assumptions turned out to be wrong is unfortunate, but far better to be methodical and clear in that manner than a lot of other rubbish you see on the arXiv. This allows science to progress faster!
If I were to draw one moral from this long story it would be that you shouldn't place too much faith in peer review by journal referees. Referees often don't read papers carefully enough, with the result that publication ends up depending on their gut feeling about the result rather than the details of the science presented therein. Gut feelings are often wrong. Hence why more transparency in the review process might be a better idea!
1 I don't want to sound critical of these other bloggers: none of them work on galactic dynamics professionally so it's perfectly natural that they shouldn't write detailed posts about it. I decided to write this mostly because it gave me a reason to learn a little bit about a new field, and to procrastinate from other stuff I was meant to do.
2 This method can only tell you about the dark matter density exactly at our location if you make some further assumptions about how this density varies with height and extrapolate to $Z\simeq0$. That's fine; if we could definitely say the existing halo models were wrong that would be exciting enough even without being certain exactly what was happening at our location.
3 Binney and Tremaine provide a nice analogy: "there are more Japanese than Nepalese in Oxford in the summer, both because the population of Japan exceeds that of Nepal, and because Japanese have larger travel budgets than Nepalese."

Following a conversation I had at lunch today about these papers, it struck me that rather than simply asserting that Moni Bidin et al (from now on, MB12) wrongly interpreted the papers they cited, I should give you the evidence and let you judge for yourselves.
ReplyDeleteMB12 cite Xue et al. (arXiv version; journal version) and Fuchs et al. (arXiv version; journal version) as evidence that $\partial\bar{V}/\partial R$ is close to zero, and even quote numerical values supposedly taken from these papers.
But Xue et al. specifically talk about the circular velocity (they call it $V_{cir}$ rather than my $V_c$), not $\bar{V}$ as you can see for yourself. The numerical value in Fuchs et al. that MB12 quote actually refers to the value of $d\ln V_c/d\ln R$, not $\partial\bar{V}/\partial R$ (see their equation 17).
MB12 also claim that this paper, this paper and this paper provide some precedent for assuming the mean azimuthal velocity curve is flat, whereas as far as I can tell all three papers actually only ever make any assumptions about the circular velocity curve (the latter two use the symbol $\Theta(R)$ rather than $V_c(R)$).
Anyway, that's my summary of the evidence. On this basis I don't see any alternative to the Bovy and Tremaine assertion that MB12 have misinterpreted the papers they cite. Have a look for yourself and see if you agree.
Great readinng this
ReplyDelete